If we define the covariant derivative of a function to coincide with the normal derivative, i.e. \({\nabla_{a}f\equiv\partial_{a}f}\), then we can use the Leibniz rule to define the covariant derivative of a 1-form. This is sometimes described as making the covariant derivative “commute with contractions,” where for a 1-form \({\varphi}\) and a vector \({v}\) we require
\begin{aligned}\nabla_{a}\left(\varphi_{b}v^{b}\right) & \equiv\left(\nabla_{a}\varphi_{b}\right)v^{b}+\varphi_{b}\left(\nabla_{a}v^{b}\right)\\
& =\left(\nabla_{a}\varphi_{b}\right)v^{b}+\varphi_{b}\left(\partial_{a}v^{b}+\Gamma^{b}{}_{ca}v^{c}\right).
\end{aligned}
At the same time, choosing a frame and treating \({\varphi_{b}}\) and \({v^{b}}\) as frame-dependent functions on \({M}\), we have
\begin{aligned}\nabla_{a}\left(\varphi_{b}v^{b}\right) & \equiv\partial_{a}\left(\varphi_{b}v^{b}\right)\\
& =\left(\partial_{a}\varphi_{b}\right)v^{b}+\varphi_{b}\left(\partial_{a}v^{b}\right),
\end{aligned}
so that equating the two we arrive at
\(\displaystyle \nabla_{a}\varphi_{b}\equiv\partial_{a}\varphi_{b}-\Gamma^{c}{}_{ba}\varphi_{c}. \)
As with vectors, the partial derivative \({\partial_{a}\varphi_{b}}\) acts upon the frame-dependent components of the 1-form.
We can then extend the covariant derivative to be a derivation on the tensor algebra by following the above logic for each covariant and contravariant component:
\begin{aligned}\nabla_{a}T^{b_{1}\ldots b_{m}}{}_{c_{1}\ldots c_{n}} & \equiv\partial_{a}T^{b_{1}\ldots b_{m}}{}_{c_{1}\ldots c_{n}}\\ & \phantom{{}=}+\underset{j=1}{\overset{m}{\sum}}\Gamma^{b_{j}}{}_{da}T^{b_{1}\ldots b_{j-1}db_{j+1}\ldots b_{m}}{}_{c_{1}\ldots c_{n}}\\ & \phantom{{}=}-\underset{j=1}{\overset{n}{\sum}}\Gamma^{d}{}_{c_{j}a}T^{b_{1}\ldots b_{m}}{}_{c_{1}\ldots c_{j-1}dc_{j+1}\ldots c_{n}} \end{aligned}
Note that since the covariant derivative of a 0-form is \({\nabla_{a}f=\partial_{a}f=\partial_{e_{a}}f=e_{a}(f)}\), we then have \({\nabla_{v}f=v^{a}\nabla_{a}f=v^{a}e_{a}(f)=v(f)}\), so that \({\nabla_{v}f=L_{v}f=\mathrm{d}f}\).
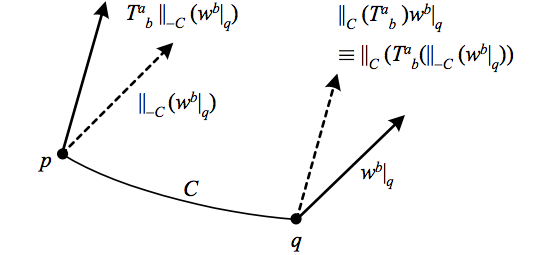
The concept of parallel transport along a curve \({C}\) can be extended to the tensor algebra as well, by parallel transporting all vector arguments backwards to the starting point of \({C}\), applying the tensor, then parallel transporting the resulting vectors forward to the endpoint of \({C}\). So for example the parallel transport of a tensor \({T^{a}{}_{b}}\) is defined as
\begin{aligned}\parallel_{C}\left(T^{a}{}_{b}\right) & \equiv\parallel^{a}{}_{c}\left(C\right)T^{c}{}_{d}\parallel^{d}{}_{b}\left(-C\right)\\
& =\left(1-\varepsilon\Gamma^{a}{}_{c}\left(v\right)\right)T^{c}{}_{d}\left(1+\varepsilon\Gamma^{d}{}_{b}\left(v\right)\right),
\end{aligned}
where for infinitesimal \({C}\) with tangent \({v}\) we have \({\parallel_{C}^{-1}=\parallel_{-C}=1+\varepsilon\check{\Gamma}\left(v\right)}\) since \({\parallel_{C}=1-\varepsilon\check{\Gamma}\left(v\right)}\).
With this definition, the covariant derivative \({\nabla_{a}T}\) can be viewed as “the difference between \({T}\) and its parallel transport in the direction \({e_{a}}\).”
| Δ It can sometimes be confusing when using the extended covariant derivative as to what type of tensor it is being applied to. For example, \({w^{b}}\) in the expression \({\partial_{a}w^{b}}\) is not a vector, it is a set of frame-dependent functions labeled by \({b}\); yet this expression can in theory also be written \({\nabla_{a}w^{b}}\), in which case there is no indication that the covariant derivative is acting on these functions instead of the vector \({w^{b}}\). |
| Δ When the covariant derivative is used as a derivation on the tensor algebra, care must be taken with relations, since their forms can change considerably based upon what arguments are applied and whether index notation is used. In particular, \({(\nabla_{a}\nabla_{b}-\nabla_{b}\nabla_{a})f=\nabla_{a}(\partial_{b}f)-\nabla_{b}(\partial_{a}f)}\) is not a “mixed partials” expression, since \({(\partial_{a}f)}\) is a 1-form. And as we will see, \({(\nabla_{a}\nabla_{b}-\nabla_{b}\nabla_{a})f}\) is a different construction than \({(\nabla_{a}\nabla_{b}-\nabla_{b}\nabla_{a})w^{c}}\), which is different from \({(\nabla_{u}\nabla_{v}-\nabla_{v}\nabla_{u})w}\). It is important to realize that an expression such as \({\nabla_{a}\nabla_{b}-\nabla_{b}\nabla_{a}}\) without context has no unambiguous meaning. |
| Δ It is important to remember that since expressions like \({\partial_{a}w^{b}}\) and \({\Gamma^{c}{}_{ba}}\) are not tensors, applying \({\nabla_{d}}\) to them is not well-defined (unless we consider them as arrays of functions and are applying \({\nabla_{d}=\partial_{d}}\)). |
| Δ It is important to remember that we may raise and lower indices in a covariant derivative expression, since \({\nabla_{c}g_{ab}=0\Rightarrow g^{ad}\nabla_{c}T_{ab}=\nabla_{c}T^{d}{}_{b}}\), but we may not do so in a partial derivative expression: \({g^{ad}\partial_{c}T_{ab}\neq\partial_{c}T^{d}{}_{b}}\). |