We now define an orientable space as one that has a triangulation with no internal boundary. So all the surfaces in the previous figure are orientable, since all the internal boundaries cancel. In a non-orientable surface, any triangulation will have at least one internal boundary that does not cancel. For example, the Möbius strip is non-orientable, since starting from a cylinder, the boundary one cuts, flips, and glues will not cancel.

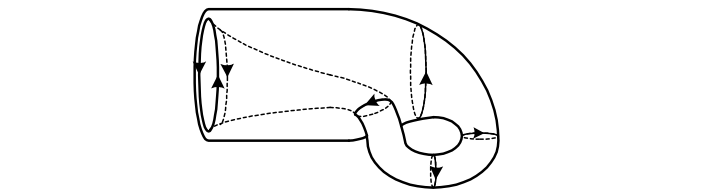
The simplest closed non-orientable surface is the Klein bottle. We can see from the preceding figure that a triangulated cylinder has external boundaries oppositely oriented. Thus in order to cancel internal boundaries when forming a surface out of cylinders, each new cylinder must begin with a boundary of the same orientation. In the following figure we illustrate building the Klein bottle out of cylinders, noting that upon return to the “mouth” at left from the “inside,” we are faced with a non-canceling internal boundary.

The other familiar non-orientable space we’ve encountered is \({\mathbb{R}\textrm{P}^{2}}\). In general, \({\mathbb{R}\textrm{P}^{n}}\) is orientable if \({n}\) is odd, and is non-orientable if \({n}\) is even.