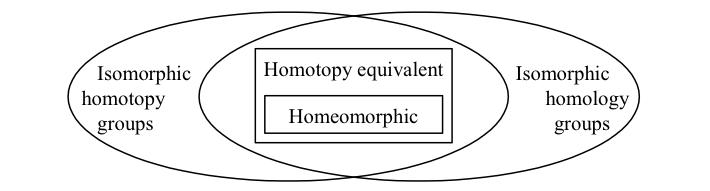
Algebraic topology is concerned with characterizing spaces. The main tools used to do this, called homotopy groups and homology groups, measure the “holes” of a space, and so are invariant under homotopy equivalence. More precisely, these objects are functors from the category of spaces and continuous maps to that of groups and homomorphisms.
One might hope that some definitive conclusion could be reached if all of these objects were isomorphic for a given space, but unfortunately this is not the case: different spaces may have identical measurements.
Thus the tools of algebraic topology are best viewed as incomplete measurements, or “shadows” of a space: if they are different, we know the spaces are distinct, but if they are the same, we cannot conclude anything in general.