The construction of the homology groups is somewhat complicated, but the idea behind it is quite intuitive. For simple spaces, we expect that \({H_{n}}\) will be a direct product of \({\mathbb{Z}}\) components, one for each “\({n}\)-dimensional hole” in \({X}\) that is not the boundary of a \({(n+1)}\)-volume, since each such hole can be wrapped around any number of times in either direction, and none of these wrappings are homologous.
| ◊ To be a bit more explicit, if \({\sigma}\) is an \({n}\)-simplex which encloses a hole and is therefore not a boundary, for every integer \({a}\) there is a homologically distinct \({n}\)-chain \({a\sigma}\) consisting of \({a}\) copies of \({\sigma}\), with the orientation reversed for negative \({a}\). |
Above, the cycle \({c_{1}}\) is the boundary of a disc, and so is homologous to a point. A hole in \({X}\) prevents \({c_{2}}\) from being the boundary of any surface. \({c_{3}}\) is homologous to \({c_{4}}\) since their difference is the boundary of an annulus, thus preventing the hole from being counted twice. Thus \({H_{1}\left(X\right)=\mathbb{Z}\oplus\mathbb{Z}}\). Note that a cycle around both holes (not depicted) would be homologous to the cycle \({c_{2}+c_{4}}\).
The best way to see this is to consider some examples.
| Homology Group | Diagram |
|---|---|
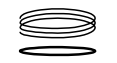
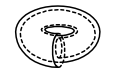
| \({H_{1}(S^{1})=\mathbb{Z}}\) |
|
| A loop can be mapped to a circle by wrapping around any number of times in either direction | |
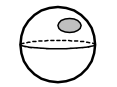
| \({H_{1}(S^{2})=0}\) |
|
| Any circle on the sphere is the boundary of a disc on the sphere | |
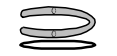
| \({H_{2}(S^{1})=0}\) |
|
| Any sphere mapped along the edge of a circle is always the boundary of a ball also mapped along the circle; similarly, any torus mapped to the circle is the boundary of a solid torus also mapped to the circle | |
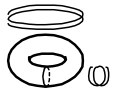
| \({H_{1}(T^{2})=\mathbb{Z}\oplus\mathbb{Z}}\) |
|
| The two circles that make up the 1-skeleton of a torus are not homologous and thus a loop can wrap around either circle any number of times in either direction | |
| \({H_{2}(T^{2})=\mathbb{Z}}\) |
|
| A torus can be mapped to itself by wrapping around any number of times in either direction | |
These calculations reflect the close relationship between homology groups and cell complex structure. Since the \({n^{\textrm{th}}}\) homology group is defined in terms of \({n}\)-surfaces, we intuitively expect \({H_{n}(X)}\) to only depend on the \({(n+1)}\)-skeleton of \({X}\) (which recall includes all \({k}\)-cells for \({k\leq n+1}\)), and this is in fact true if \({X}\) is a cell complex. Thus if \({X}\) is a cell complex with finitely many cells, for example a closed manifold, \({H_{n}(X)}\) is a finitely generated group.
For example, inductively extending the first three observations to spheres in arbitrary dimension shows that \({H_{n}(S^{d})=\mathbb{Z}}\) if \({n=d}\), 0 otherwise. For the \({d}\)-dimensional torus \({T^{d}}\), \({H_{n}(T^{d})}\) is the direct sum of \({c}\) copies of \({\mathbb{Z}}\) with \({c}\) the binomial coefficient \({d}\) choose \({n}\).