We first define the form versions of cycles and boundaries in homology:
- Closed form: an element of \({\textrm{Ker d}}\), i.e. a form \({\varphi}\) such that \({\mathrm{d}\varphi=0}\)
- Exact form: an element of \({\textrm{Im d}}\), i.e. a form \({\varphi}\) such that \({\varphi=\mathrm{d}\psi}\)
In this context, the term Poincaré lemma can refer to either the property “exact \({\Rightarrow}\) closed” \({(\mathrm{d}^{2}=0)}\), or the converse statement “closed \({\Rightarrow}\) exact” under certain topological conditions, which we address next.
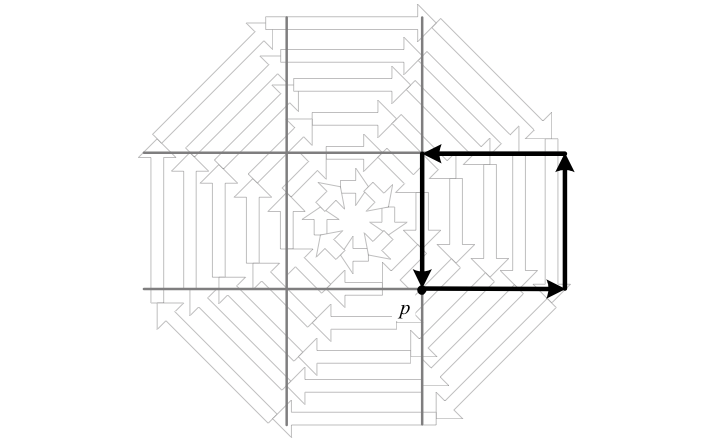
Let us try to picture a closed 1-form that is not exact using a coordinate frame. If the 1-form \({\varphi}\) is closed, it integrates to zero around any coordinate square; but if it is not exact, it does not define a function \({f}\) via \({\varphi=\mathrm{d}f}\). This means there must be a square around which adding up the values of \({\varphi}\) does not vanish. Therefore there must be a square that cannot be built from coordinate squares, i.e. there must be a “hole” in \({M}\).
A closed 1-form must vanish when integrated around any coordinate square, as for example in the square sketched above. For this same 1-form not to be exact, there must be a square around which the integral does not vanish, i.e. a square that is not a coordinate square. Above, the central square is not a coordinate square, since for the depicted 1-form to be smooth, the singular point at the center must be missing from the manifold.
This picture is confirmed and made precise by the Poincaré lemma, which states that if \({M}\) is contractible, all closed forms are exact. Recall that a contractible space is homotopy equivalent to a point, so that all \({H_{n}}\) vanish. Thus the Poincaré lemma says “on a manifold with no holes, closed and exact forms are the same thing.” In particular, any point on a manifold is contained in a coordinate chart, which is a contractible neighborhood; thus given a closed form \({\mathrm{d}\varphi=0}\) and a point \({p}\), there is always a neighborhood of \({p}\) in which we can define \({\psi}\) such that \({\varphi=\mathrm{d}\psi}\).