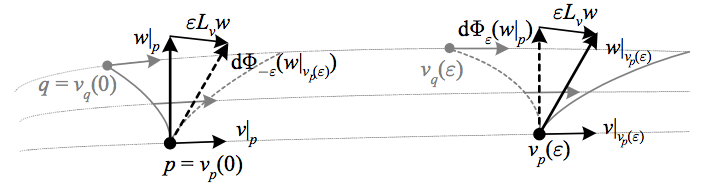Without some kind of additional structure, there is no way to “transport” vectors, or compare them at different points on a manifold, and therefore no way to construct a vector derivative. The simplest way to introduce this structure is via another vector field, which leads us to the Lie derivative \({L_{v}w\equiv\left[v,w\right]}\); as noted above, \({L_{v}}\) is a derivation on \({\mathrm{vect}(M)}\) due to the Jacobi identity. In this section we define the Lie derivative in terms of infinitesimal vector transport, and explore its geometrical meaning.
Given any vector field \({v}\) on \({M^{n}}\), it can be shown ([18] p. 37) that there exists a locally unique parameterized curve \({v_{p}(t)}\) at every point \({p\in M}\) such that \({v_{p}(0)=p}\) and \({\dot{v}_{p}(t)}\) is the value of the vector field \({v}\) at the point \({v_{p}(t)}\) (the dot indicates the derivative with respect to \({t}\), which as usual is calculated on the curve mapped to \({\mathbb{R}^{n}}\) by the coordinate chart). Each curve in this family is in general only well-defined locally, i.e. for \({-\varepsilon<t<\varepsilon}\), and is thus called the local flow of \({v}\).
For a fixed value of \({t}\), there is some region \({U\subset M}\) where the map \({\Phi_{t}\colon U\to U}\) defined by \({p\mapsto v_{p}\left(t\right)}\) on all of \({M}\) is a diffeomorphism, and within the valid domain of \({t}\) the maps \({\Phi_{t}}\) satisfy the abelian group law \({\Phi_{t}\circ\Phi_{s}=\Phi_{t+s}}\); thus the \({\Phi_{t}}\) are called a local one-parameter group of diffeomorphisms. This name is somewhat misleading, since due to the limited valid domain of \({t}\) the maps \({\Phi_{t}}\) do not actually form a group; the “local” reflects the fact that the diffeomorphisms are not on all of \({M}\). In the case that these maps are in fact valid for all of \({t}\) and \({M}\), \({v}\) is called a complete vector field, and the \({\Phi_{t}}\) are called a one-parameter group of diffeomorphisms. If \({M}\) is compact, then every vector field is complete; if not, then a vector field is complete if it has compact support (is zero except on a compact subset of \({M}\)).
The tangent map \({\mathrm{d}\Phi}\) defined by the vector field \({v}\) is then the extra structure we need to “transport” vectors. \({\mathrm{d}\Phi}\) maps a vector tangent to the curve \({C}\) to a vector tangent to the curve \({\Phi\left(C\right)}\); it “pushes vectors along the flow of \({v}\).” We can now define the Lie derivative as a limit
\begin{aligned}L_{v}w&\equiv\underset{\varepsilon\rightarrow0}{\textrm{lim}}\frac{1}{\varepsilon}\left[\mathrm{d}\Phi_{-\varepsilon}\left(w\left|_{v_{p}\left(\varepsilon\right)}\right.\right)-w\left|_{p}\right.\right]\\&=\underset{\varepsilon\rightarrow0}{\textrm{lim}}\frac{1}{\varepsilon}\left[w\left|_{v_{p}\left(\varepsilon\right)}\right.-\mathrm{d}\Phi_{\varepsilon}\left(w\left|_{p}\right.\right)\right]\\&=\underset{\varepsilon\rightarrow0}{\textrm{lim}}\frac{1}{\varepsilon}\left[w\left|_{p}\right.-\mathrm{d}\Phi_{\varepsilon}\left(w\left|_{v_{p}\left(-\varepsilon\right)}\right.\right)\right].
\end{aligned}
The Lie derivative \({L_{v}w}\) is “the difference between \({w}\) and its transport by the local flow of \({v}\).”
| ◊ In this and future depictions of vector derivatives, the situation is simplified by focusing on the change in the vector field \({w}\) while showing the “transport” of \({w}\) as a parallel displacement. This has the advantage of highlighting the equivalency of defining the derivative at either 0 or \({\varepsilon}\) in the limit \({\varepsilon\rightarrow0}\). Depicting \({L_{v}w}\) as a non-parallel vector at \({v_{p}\left(t\right)}\) would be more accurate, but would obscure this fact. We also will follow the picture here in using words to characterize derivatives: namely, “the difference” is short for “the difference per unit \({\varepsilon}\) to order \({\varepsilon}\) in the limit \({\varepsilon\rightarrow0}\).” |
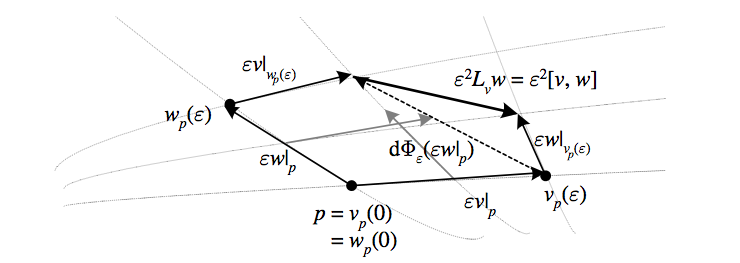
This definition can be shown to be equivalent to \({L_{v}w\equiv\left[v,w\right]}\). Another way of depicting the Lie derivative that highlights the anti-commutativity of the Lie bracket is to consider \({L_{v}w}\) in terms of a loop defined by the flows of \({v}\) and \({w}\), noting that \({v_{p}(\varepsilon)=p+\varepsilon v}\).
The above depicts the Lie derivative \({L_{v}w}\) as the vector field whose local flow is the “commutator of the flows of \({v}\) and \({w}\),” i.e. it is the difference between the local flow of \({v}\) followed by \({w}\) and that of \({w}\) followed by \({v}\). Thus \({L_{v}w}\) “completes the parallelogram” formed by the flow lines.