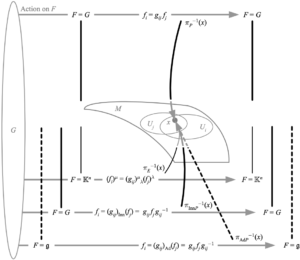
If two \({G}\)-bundles \({(E,M,F)}\) and \({(E^{\prime},M,F^{\prime})}\), with the same base space and structure group, also share the same trivializing neighborhoods and transition functions, then they are each called an associated bundle with regard to the other. It is possible to construct (up to isomorphism) a unique principal \({G}\)-bundle associated to a given \({G}\)-bundle; going in the other direction, given a principal \({G}\)-bundle and a left action of \({G}\) on a fiber \({F}\), we can construct a unique associated \({G}\)-bundle with fiber \({F}\). In particular, given a principal bundle \({(P,M,G)}\), the rep of \({G}\) on itself by inner automorphisms defines an associated bundle \({(\mathrm{Inn}P,M,G)}\), and the adjoint rep of \({G}\) on \({\mathfrak{g}}\) defines an associated bundle \({(\mathrm{Ad}P,M,\mathfrak{g})}\). If \({G}\) has a linear rep on a vector space \({\mathbb{K}^{n}}\), this rep defines an associated bundle \({(E,M,\mathbb{K}^{n})}\), which we explore next.
The above depicts how given a principal bundle, we can construct an associated bundle for the action of \({G}\) on a vector space \({\mathbb{K}^{n}}\) by a linear rep, on itself by inner automorphisms, and on its Lie algebra \({\mathfrak{g}}\) by the adjoint rep. The action of the structure group is shown in general and for the case in which \({G}\) is a matrix group, with matrix multiplication denoted as juxtaposition. Although denoted identically, the \({f_{i}}\) are those corresponding to each bundle.
| Δ The \({G}\)-bundle \({E}\) with fiber \({F}\) associated to a principal bundle \({P}\) is sometimes written \({E=P\times_{G}F\equiv(P\times F)/G}\), where the quotient space collapses all points in the product space which are related by the right action of some \({g\in G}\) on \({P}\) and the right action of \({g^{-1}}\) on \({F}\). |