A group action (AKA left action, realization, representation) of any group \({G}\) on any set \({X}\) is a homomorphism \({\rho\colon G\to\textrm{Aut}\left(X\right)}\), where \({\textrm{Aut}\left(X\right)}\) is the group of automorphisms of \({X}\) (the symmetry group). Since in most applications a group action is fixed, we will write the action of \({g\in G}\) on \({x\in X}\) as simply \({g(x)}\), or \({g_{\rho}\left(x\right)}\) if the homomorphism needs to be made explicit; other common notations are \({gx}\), \({\rho_{g}(x)}\) and \({\rho(g)(x)}\). When acted on by \({G}\), \({X}\) is sometimes called a G-set (or a G-space if it is a space).
| Δ As we will see, some specific types of actions (e.g. reps) may be required to preserve additional structures that exist on \({X}\) (e.g. a vector space structure), but in general, the automorphism group is that of \({X}\) as a set or space, with any additional structure (e.g. that of a fiber bundle) disregarded. |
Since a left action is a homomorphism, \({g\circ h}\) and \({gh}\) are required to be the same automorphism, i.e.
\(\displaystyle g\left(h\left(x\right)\right)=\left(gh\right)\left(x\right)\:\forall x\in X. \)
A right action operates from the right within the group, and so instead requires that
\(\displaystyle g\left(h\left(x\right)\right)=\left(hg\right)\left(x\right), \)
and is often written \({xg}\). Note that a left action can be turned into a right action (and vice versa) via the inverse; e.g. if \({G}\) has a left action and we define a new action \({g_{R}(x)\equiv g^{-1}(x)}\), then
\(\displaystyle \begin{aligned}g_{R}\left(h_{R}\left(x\right)\right) & =g^{-1}\left(h^{-1}(x)\right) \\ & =(g^{-1}h^{-1})(x) \\ & =(hg)^{-1}(x) \\ & =\left(hg\right)_{R}\left(x\right). \end{aligned} \)
Some definitions related to a group action are:
- Orbit of \({x\in X}\): \({\textrm{orbit}(x)\equiv\left\{ g(x)\mid g\in G\right\} }\); i.e. all points of \({X}\) that can be reached from \({x}\) by the action of some \({g}\)
- Isotropy group (AKA little group, stabilizer subgroup) of \({x}\): the subgroup \({I\left(x\right)\equiv\left\{ g\mid g\left(x\right)=x\right\} }\); i.e. all elements of \({G}\) that leave \({x}\) fixed
- Transitive action: \({\forall x,y\:\exists g\mid y=g\left(x\right)\Leftrightarrow X}\) is a single orbit; i.e. any two points are related by the action of some \({g}\)
- Faithful (AKA effective) action: \({\forall g\neq h\:\exists x\mid g(x)\neq h(x)\Leftrightarrow\rho}\) is injective; i.e. every \({g}\) is mapped to a distinct automorphism
- Free (AKA semiregular, fixed point free) action: \({\forall g\neq h,\: g(x)\neq h(x)\:\forall x\Leftrightarrow}\) only \({e}\) has a fixed point; i.e. the orbit of every \({x}\) is an injective map of \({G}\)
- Regular (AKA simply transitive, sharply transitive) action: \({\forall x,y\:\exists}\) unique \({g\mid y=g(x)\Leftrightarrow}\) transitive and free; i.e. any two points are related by the action of one \({g}\)
One can state various relationships between these properties, for example: free implies faithful; free is equivalent to all isotropy groups being trivial; and \({G}\) acts transitively on any orbit of \({X}\). If the action of \({G}\) is transitive, then \({X}\) is called a homogeneous space for \({G}\); if the action is also free (i.e. regular), then \({X}\) is called a principal homogeneous space or G-torsor. A \({G}\)-torsor is isomorphic to \({G}\) as a set or space, but there is no uniquely defined identity element; it can thus be thought of as a group “with the identity forgotten.” The action of \({G}\) on itself by left or right multiplication is regular.
| Δ These concepts highlight potential confusions around \({\mathbb{R}^{n}}\) as a vector space, Lie group, and manifold: the action of the Lie group of vectors under addition \({\mathbb{R}^{n}}\) on the manifold \({\mathbb{R}^{n}}\) by displacement is regular, making the manifold a \({\mathbb{R}^{n}}\)-torsor, i.e. it is isomorphic to the Lie group \({\mathbb{R}^{n}}\) but with the origin forgotten. |
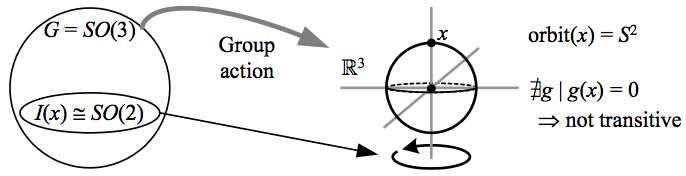
The above depicts how the action of the three dimensional rotations \({SO(3)}\) on \({\mathbb{R}^{3}}\) is not transitive, since two points at different radii cannot be reached from each other by the action of a rotation; is faithful, since every rotation is a distinct automorphism; but is not free, since every rotation leaves an axial line fixed. The orbit of \({x}\) is the sphere of the same radius, and the isotropy group of \({x}\) is the two dimensional rotations around the axis it determines.
If a group \({G}\) has a left action on two sets \({X}\) and \({Y}\), a mapping \({f\colon X\to Y}\) is called equivariant if
\(\displaystyle f\left(g\left(x\right)\right)=g\left(f\left(x\right)\right) \)
for all \({g}\) and \({x}\). In other words, an equivariant map is a homomorphism with respect to the group action; it is therefore also sometimes called a G-map or G-homomorphism. This definition has to be modified if we extend it to right actions, where we take advantage of the property \({(gh)^{-1}=h^{-1}g^{-1}}\) to maintain ordering:
| Left action on \({Y}\) | Right action on \({Y}\) | |
|---|---|---|
| Left action on \({X}\) | \({\begin{aligned}f\left(g\left(x\right)\right) & =g\left(f\left(x\right)\right)\\ f(gx) & =gf(x) \end{aligned}}\) | \({\begin{aligned}f\left(g\left(x\right)\right) & =g^{-1}\left(f\left(x\right)\right)\\ f(gx) & =f(x)g^{-1} \end{aligned}}\) |
| Right action on \({X}\) | \({\begin{aligned}f\left(g\left(x\right)\right) & =g^{-1}\left(f\left(x\right)\right)\\ f(xg) & =g^{-1}f(x) \end{aligned}}\) | \({\begin{aligned}f\left(g\left(x\right)\right) & =g\left(f\left(x\right)\right)\\ f(xg) & =f(x)g \end{aligned}}\) |
The equivariance condition for a map \({f\colon X\to Y}\) between two \({G}\)-sets, using two common notations.
If \({G}\) has a left action on \({X}\), and we denote the left cosets of the isotropy group as \({G/I(x)}\), then the map \({f:G/I(x)\rightarrow\mathrm{orbit}(x)}\) defined by \({gI(x)\mapsto gx}\) is equivariant. The orbit-stabilizer theorem states that this map is also bijective. Such a map is sometimes called a \({G}\)-map isomorphism. For finite \({G}\), the corollary \({\left|G\right|/\left|I(x)\right|=\left|G:I(x)\right|=\left|\mathrm{orbit}(x)\right|}\) is also sometimes referred to as the orbit-stabilizer theorem, where \({\left|\mathrm{orbit}(x)\right|}\) denotes the number of elements in the set.
A Lie group has the additional structure of a differentiable manifold, which is required to carry over the action homomorphism to the corresponding automorphisms. Thus a Lie group action is defined to be a smooth homomorphism from a Lie group \({G}\) to \({\textrm{Diff}(M)}\), the Lie group of diffeomorphisms of a manifold \({M}\).