In Euclidean space (of any dimension), we can write any element \({U=\textrm{exp}\left(B\right)}\) of \({\textrm{Spin}(n,0)}\) in terms of “unit” 2-blades \({\hat{B}_{i}^{2}=-1}\) as \({U=\textrm{exp}\left(-\theta^{i}\hat{B}_{i}/2\right)}\). Under the homomorphism \({R}\), it is not hard to show that this element then corresponds to active rotations by \({\theta^{i}}\) in the planes defined by the 2-blades \({\hat{B}_{i}}\).
In 2 dimensions, if \({\hat{B}=\hat{e}_{1}\hat{e}_{2}=\hat{e}_{1}\wedge\hat{e}_{2}}\), then
\(\displaystyle U=\textrm{exp}\left(-\frac{\theta}{2}\hat{e}_{1}\hat{e}_{2}\right)=\cos\left(\frac{\theta}{2}\right)-\sin\left(\frac{\theta}{2}\right)\hat{e}_{1}\hat{e}_{2}, \)
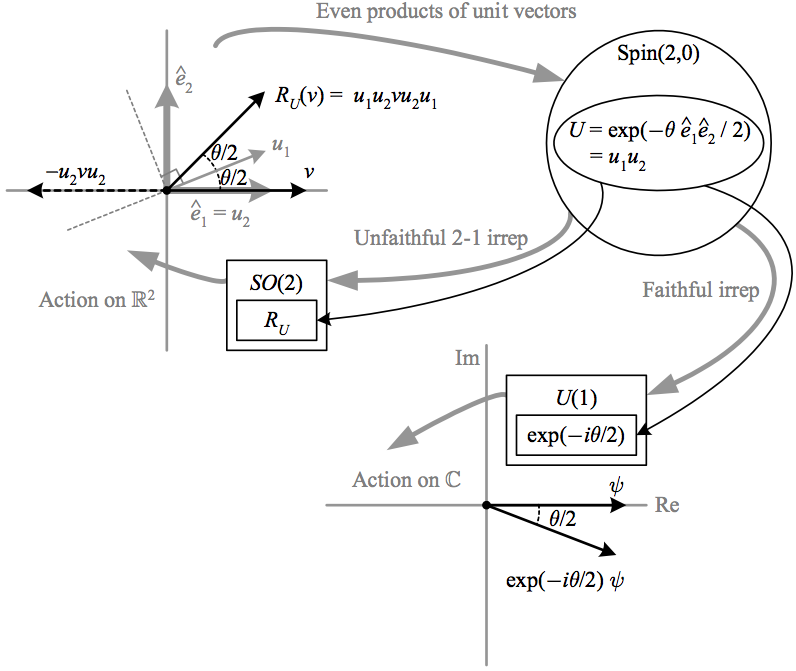
and \({R_{U}(v)=UvU^{-1}}\) can be seen to be a rotation of \({v}\) by \({\theta}\), whose direction is from \({\hat{e}_{1}}\) towards \({\hat{e}_{2}}\). Thus this element can also be written as \({U=u_{1}u_{2}}\), the Clifford product of two unit vectors separated by an angle of \({\theta/2}\), which corresponds to the same rotation \({R_{U}(v)=Uv\widetilde{U}=u_{1}u_{2}vu_{2}u_{1}}\). Since \({\hat{B}^{2}=-1}\), it naturally maps to \({i}\) in the rep on \({U(1)}\), thus corresponding to a spinor “rotation” of \({\theta/2}\).
The above depicts how an element \({U=\exp(-\theta\hat{e}_{1}\hat{e}_{2}/2)=u_{1}u_{2}}\) of \({\textrm{Spin}(2,0)}\) corresponds to a rotation by \({\theta}\) which can be written \({R_{U}(v)=\exp(-\theta\hat{e}_{1}\hat{e}_{2}/2)v\exp(+\theta\hat{e}_{1}\hat{e}_{2}/2)=u_{1}u_{2}vu_{2}u_{1}}\), where \({u_{1}}\) and \({u_{2}}\) are unit vectors separated by an angle of \({\theta/2}\). Since the “rotation” in \({U(1)}\) is by only \({\theta/2}\), a complete rotation in \({\mathbb{R}^{2}}\) corresponds to half of one in \({\mathbb{C}}\), i.e. for \({\theta=2\pi}\), \({\exp(-i2\pi/2)=-1}\).
| Δ In arbitrary dimension and signature, the idea that a spinor “rotation” by \({\theta/2}\) corresponds to a rotation by \({\theta}\) is less clear; but it is always true that a spinor sign reversal corresponds to a return to the original state (e.g. a rotation by \({2\pi}\)), since \({U=-1}\) corresponds to \({R_{U}(v)=(-1)v(-1)=v}\). |
In 3 dimensions, we can choose an orthonormal basis \({\hat{e}_{i}}\) and write the element as
\(\displaystyle U=\textrm{exp}\left(-\sum\frac{\theta^{i}}{2}\hat{e}_{j}\hat{e}_{k}\right), \)
where the unit vector \({\hat{u}=\hat{u}^{i}\hat{e}_{i}}\) is defined by \({\theta\hat{u}^{i}\equiv\theta^{i}}\), the sum is over all indices \({\{i,j,k\}}\) that are even permutations of \({\{1,2,3\}}\), and \({U}\) can be seen to correspond to a rotation by \({\theta}\) in the plane perpendicular to \({\hat{u}}\). Note that we cannot split this into a product of exponentials, since these bivectors do not commute. However if we start with the transformation instead of the basis, we can express it as the exponential of a single 2-blade in the plane of rotation.
In spacetime, an element \({U}\) of \({\textrm{Spin}(3,1)^{e}}\) corresponds to a restricted (i.e. proper orthochronous) Lorentz transformation, an element of \({SO(3,1)^{e}}\). Choosing an orthonormal basis \({\hat{e}_{\mu}}\), a boost of rapidity \({\phi}\) in the direction of the unit vector \({\hat{v}=\hat{v}^{i}\hat{e}_{i}}\) corresponds to the element \({\textrm{exp}(-\phi^{i}\hat{e}_{0}\hat{e}_{i}/2)}\) of \({\textrm{Spin}(3,1)^{e}}\), where \({\phi^{i}\equiv\phi\hat{v}^{i}}\). Similarly, a rotation by \({\theta}\) in the space-like plane perpendicular to \({\hat{u}=\hat{u}^{i}\hat{e}_{i}}\) corresponds to the element \({\textrm{exp}(-\theta^{i}\Omega\hat{e}_{0}\hat{e}_{i}/2)}\), where \({\theta^{i}\equiv\theta\hat{u}^{i}}\). Any element of \({\textrm{Spin}(3,1)^{e}}\) can then be written
\(\displaystyle U=\pm\textrm{exp}\left(-\frac{\phi^{i}}{2}\hat{e}_{0}\hat{e}_{i}-\frac{\theta^{i}}{2}\Omega\hat{e}_{0}\hat{e}_{i}\right). \)
Note that this decomposition into boost and rotation terms depends on the specific basis, and that again we cannot split this into a product of exponentials, since since \({\hat{e}_{0}\hat{e}_{i}}\) and \({\hat{e}_{0}\hat{e}_{j}}\) do not commute.
If we start with a transformation \({U}\) instead of a basis, we can then choose a basis that lets us split the exponential factors. We know that \({U}\) is of the form \({\pm\textrm{exp}(B)}\), where \({B}\) is a bivector in \({C(3,1)}\). It is not hard to show that any non-null bivector \({B^{2}\neq0}\) can be written in the form \({B=-\phi\hat{B}/2-\theta\Omega\hat{B}/2}\), where \({\hat{B}^{2}=1}\). Since \({\Omega}\) commutes with any bivector and \({\Omega^{2}=-1}\), it acts like the imaginary unit \({\sqrt{-1}}\), and the multiplication of exponentials follows the scalar rule. We can thus write \({U}\) in the form
\(\displaystyle U=\textrm{exp}\left(-\frac{\phi}{2}\hat{B}\right)\textrm{exp}\left(-\frac{\theta}{2}\Omega\hat{B}\right). \)
Note that we have dropped the \({\pm}\) factor since \({-\textrm{exp}\left(i\theta\right)=\textrm{exp}\left(i\left(\theta-\pi\right)\right)}\).
This decomposition means that \({U}\) determines a class of orthonormal basis vectors for \({\mathbb{R}^{4}}\) in which \({\hat{B}=\hat{e}_{0}\hat{v}}\), where \({v}\) is a unit vector in space \({\hat{e}_{1}\hat{e}_{2}\hat{e}_{3}}\). In such a basis, the first term corresponds to a Lorentz boost of rapidity \({\phi}\) in the \({\hat{v}}\) direction, and the second term corresponds to a rotation by \({\theta}\) in the space-like plane perpendicular to \({\hat{v}}\). These orthogonal planes are invariant under the total transformation, i.e. vectors in these planes remain in them.
The above decomposition fails in the case \({B^{2}=0}\) because this corresponds to a “light-like” or “parabolic” Lorentz transformation, which leaves a single null plane (orthogonal to itself) invariant. This case is also the reason why the general form has to be prefixed by the \({\pm}\) factor.
| Δ It is important to remember that the treatment here is for active rotations. Passive rotations (those that rotate the coordinate axes while leaving the vector fixed) are in the opposite direction, so to represent them we would multiply both angles by \({-1}\) in the above expressions. |